Die CAUCHY-SCHWARZsche Ungleichung gilt für alle reellen Zahlen 
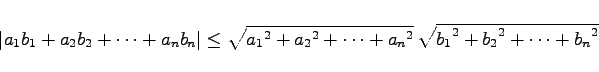 |
(1.117a) |
oder
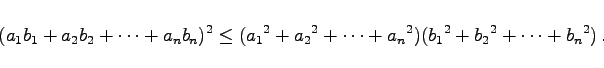 |
(1.117b) |
Für zwei endliche Zahlenfolgen mit jeweils n Zahlen ist der Betrag der Summe ihrer paarweisen Produkte kleiner oder gleich dem Produkt der beiden Quadratwurzeln aus den Summen der Quadrate dieser Zahlen. Das Gleichheitszeichen gilt nur für  .
.
Wenn n =3 ist und {a1, a2, a3} und {b1, b2, b3} als rechtwinklige kartesische Koordinaten von Vektoren aufgefaßt werden, dann besagt die Ungleichung von CAUCHY-SCHWARZ, daß das skalare Produkt zweier Vektoren betragsmäßig kleiner oder gleich dem Produkt der Beträge dieser Vektoren ist. Wenn n >3 ist, dann kann diese Aussage auf Vektoren im n-dimensionalen euklidischen Raum ausgedehnt werden.
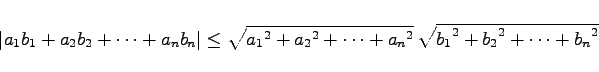
![]() .
.
![]() werden die konjugiert komplexen Zahlen zu
werden die konjugiert komplexen Zahlen zu ![]() bezeichnet.
bezeichnet.
