Allgemeiner Fall der Ungleichung 2. Grades

ax2 +bx + c > 0 (1.132a)


oder

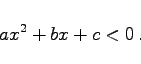(1.132b)

Die Ungleichung wird durch a dividiert, wobei sich das Vorzeichen im Falle a < 0 ändert, so daß sie auf die Form

x2 +px + q < 0 (1.132c)


oder

x2 + px + q > 0 (1.132d)


gebracht wird. Durch quadratische Ergänzung folgt

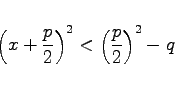(1.132e)

oder

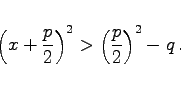(1.132f)

Bezeichnet man nun 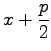mit z und 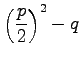mit m, dann ergibt sich die Ungleichung

z2 < m (1.132g)


oder

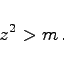(1.132h)

Nachdem diese gelöst ist, kann x bestimmt werden.

Beispiel A


Die Lösung ist

Beispiel B

    Die Ungleichung ist identisch erfüllt.
Beispiel C

und Die Lösungsbereiche sind x > 5 und .