Inhalt Index DeskTop Bronstein
![]()
![]() Variationsrechnung Variationsaufgaben mit Funktionen mehrerer Veränderlicher
Variationsrechnung Variationsaufgaben mit Funktionen mehrerer Veränderlicher
Eine der einfachsten Aufgaben mit Funktion von mehreren Variablen stellt das folgende Variationsproblem für ein Doppelintegral dar:
Dabei soll die gesuchte Funktion u =u(x,y) auf dem Rand ![]() des Bereiches G gegebene Werte annehmen. Analog zum Abschnitt EULERsche Differentialgleichung werden Vergleichsfunktionen der Form
des Bereiches G gegebene Werte annehmen. Analog zum Abschnitt EULERsche Differentialgleichung werden Vergleichsfunktionen der Form
angesetzt, wobei u0(x,y) eine Lösung der Variationsaufgabe (10.44) ist und die vorgegebenen Randwerte annimmt, während ![]() die Bedingung
die Bedingung
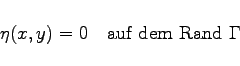 |
(10.46) |
erfüllt und wie u0(x,y) entsprechend oft partiell differenzierbar ist.
Die Größe ![]() ist ein Parameter. Durch u =u(x,y) wird eine Fläche beschrieben, die der Lösungsfläche u0(x,y) benachbart ist. Mit (10.45) geht I[u] in
ist ein Parameter. Durch u =u(x,y) wird eine Fläche beschrieben, die der Lösungsfläche u0(x,y) benachbart ist. Mit (10.45) geht I[u] in ![]() über, d.h., aus der Variationsaufgabe (10.44) wird eine Extremwertaufgabe, die die notwendige Bedingung
über, d.h., aus der Variationsaufgabe (10.44) wird eine Extremwertaufgabe, die die notwendige Bedingung
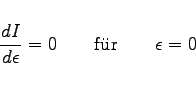 |
(10.47) |
erfüllen muß. Daraus folgt die EULERsche Differentialgleichung
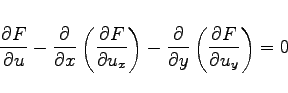 |
(10.48) |
als notwendige Bedingung für die Lösung der Variationsaufgabe (10.44).
| Beispiel |
|
Eine unbelastete Membran, die am Rand |
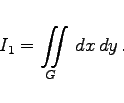 |
(10.49a) |
Wird die Membran durch eine Belastung so deformiert, daß jeder Punkt eine Auslenkung u =u(x,y) in z-Richtung erfährt, dann wird ihr Flächeninhalt nach der Formel
berechnet. Linearisiert man den Integranden in (10.49b) nach TAYLOR, dann erhält man die Beziehung
 |
(10.49c) |
Für die potentielle Energie U der deformierten Membran gilt
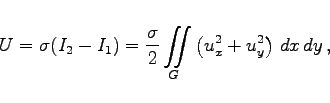 |
(10.49d) |
wobei die Konstante ![]() als Spannung der Membran bezeichnet wird. Auf diese Weise entsteht das sogenannte DIRICHLETsche Variationsproblem: Die Funktion u=u(x,y) ist so zu bestimmen, daß sie das Funktional
als Spannung der Membran bezeichnet wird. Auf diese Weise entsteht das sogenannte DIRICHLETsche Variationsproblem: Die Funktion u=u(x,y) ist so zu bestimmen, daß sie das Funktional
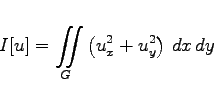 |
(10.49e) |
zu einem Extremum macht und auf dem Rand ![]() des ebenen Gebietes G verschwindet. Die zugehörige EULERsche Differentialgleichung lautet
des ebenen Gebietes G verschwindet. Die zugehörige EULERsche Differentialgleichung lautet
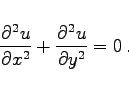 |
(10.49f) |
Es handelt sich um die LAPLACEsche Differentialgleichung für Funktionen von zwei Variablen.