Inhalt Index DeskTop Bronstein
![]()
![]() Funktionentheorie Berechnung reeller Integrale durch Integration im Komplexen Anwendungen des Lemmas von Jordan
Funktionentheorie Berechnung reeller Integrale durch Integration im Komplexen Anwendungen des Lemmas von Jordan
In vielen Fällen lassen sich reelle uneigentliche Integrale mit unbeschränktem Integrationsgebiet durch komplexe Integrale über geschlossene Wege berechnen. Um dabei immer wiederkehrende Abschätzungen zu vermeiden, benutzt man das Lemma von JORDAN, das sich auf Integrale der Form
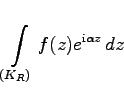
Das Lemma von JORDAN unterscheidet folgende Fälle:
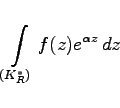 |
(14.58b) |
vor, wenn K*R einen Halbkreis bzw. Teilbogen in der linken Halbebene mit ![]() darstellt, bzw in der rechten mit
darstellt, bzw in der rechten mit ![]() .
.