Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Diskrete dynamische Optimierung Beispiele diskreter Entscheidungsmodelle
Optimierung Diskrete dynamische Optimierung Beispiele diskreter Entscheidungsmodelle
In der j-ten Periode eines in n Stufen unterteilbaren Zeitraumes benötigt ein Betrieb vj Mengeneinheiten eines bestimmten Ausgangsstoffes. Zu Beginn einer Periode j sei dieser Stoff in der Menge xj-1 vorrätig, speziell sei x0 = xa vorgegeben. Davon ausgehend ist eine Entscheidung darüber zu treffen, welche Menge uj zum Preis cj pro Mengeneinheit einzukaufen ist. Dabei darf die vorhandene Lagerkapazität K nicht überschritten werden, d.h. ![]() . Gesucht ist eine Einkaufspolitik
. Gesucht ist eine Einkaufspolitik ![]() , die die Gesamtkosten minimiert. Dies führt auf das folgende dynamische Problem:
, die die Gesamtkosten minimiert. Dies führt auf das folgende dynamische Problem:
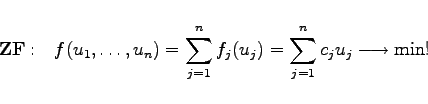 |
(18.124a) |
In (18.124b) ist berücksichtigt, daß der Bedarf immer gedeckt ist und die Lagerkapazität nicht überschritten wird. Enstehen zusätzlich Lagerkosten l pro Mengeneinheit und Periode, dann betragen die mittleren Lagerkosten in der j-ten Periode ![]() , und die modifizierte Kostenfunktion lautet
, und die modifizierte Kostenfunktion lautet
 |
(18.125) |