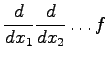Berechnung von Differentialquotienten
Der Differentiationsoperator wurde als  eingeführt. Seine vollständige Schreibweise lautet
eingeführt. Seine vollständige Schreibweise lautet
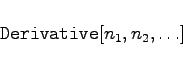 |
(20.71) |
Die Argumente geben an, wie oft nach der jeweiligen Variablen differenziert werden soll. In diesem Sinne handelt es sich um einen Operator der partiellen Differentiation. Mathematica versucht die Darstellung des Ergebnisses als reine Funktion.
Die Differentiation einer vorgegebenen Funktion kann vereinfachend durch den Operator  durchgeführt werden. Mit
durchgeführt werden. Mit  wird die Ableitung der Funktion f(x) angegeben.
wird die Ableitung der Funktion f(x) angegeben.
 gehört zu einer Gruppe von Differentialoperationen, die in der folgenden Tabelle aufgeführt sind.
gehört zu einer Gruppe von Differentialoperationen, die in der folgenden Tabelle aufgeführt sind.
Tabelle Operationen der Differentiation
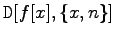 |
liefert die n-te Ableitung der Funktion f(x). Entsprechend liefern: |
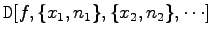 |
mehrfache Ableitungen jeweils ni-mal nach 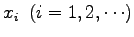 |
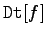 |
das vollständige Differential der Funktion f |
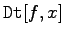 |
die vollständige Ableitung  der Funktion der Funktion |
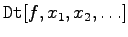 |
die vollständige Ableitung einer Funktion mehrerer Veränderlicher
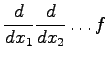 |
Die Anweisung  liefert die vollständige Ableitung bzw. das vollständige Differential.
liefert die vollständige Ableitung bzw. das vollständige Differential.
| Beispiel D |
|
Mathematica nimmt in diesen letzten Beispielen an, daß y eine Funktion von x ist, die es jedoch nicht kennt, und schreibt den zweiten Teil der Ableitung deshalb wieder symbolisch.
|
Wenn Mathematica bei der Differentiation auf eine symbolische Funktion stößt, beläßt es diese in der allgemeinen Form und drückt die Ableitung in der Form f' aus.
Mathematica kennt die Regeln für die Differentiation von Produkten, Quotienten und die Kettenregel und kann diese auch formal anwenden:
![]()
![]() Computeralgebrasysteme Anwendungen von Computeralgebrasystemen Differential- und Integralrechnung Mathematica
Computeralgebrasysteme Anwendungen von Computeralgebrasystemen Differential- und Integralrechnung Mathematica
![]() eingeführt. Seine vollständige Schreibweise lautet
eingeführt. Seine vollständige Schreibweise lautet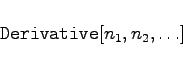
![]() durchgeführt werden. Mit
durchgeführt werden. Mit ![]() wird die Ableitung der Funktion f(x) angegeben.
wird die Ableitung der Funktion f(x) angegeben.![]() gehört zu einer Gruppe von Differentialoperationen, die in der folgenden Tabelle aufgeführt sind.
gehört zu einer Gruppe von Differentialoperationen, die in der folgenden Tabelle aufgeführt sind.