Inhalt Index DeskTop Bronstein
![]()
![]() Computeralgebrasysteme Mathematica Zahlenarten in Mathematica
Computeralgebrasysteme Mathematica Zahlenarten in Mathematica
Mathematica kennt vier Arten von Zahlen, die in der folgenden Tabelle dargestellt sind.
| Zahlenart | Kopf | Charakteristik | Eingabe |
| Ganze Zahlen | exakte ganze Zahl beliebiger Länge | nnnnn | |
| Rationale Zahlen | teilerfremder Bruch der Form |
pppp/qqqq | |
| Reelle Zahlen | Gleitpunktzahl beliebiger spezifierter Präzision | nnnn.mmmm | |
| Komplexe Zahlen | komplexe Zahl der Form zahl + zahl |
Reelle Zahlen, d.h. Gleitpunktzahlen, dürfen beliebige Länge haben. Wird eine ganze Zahl nnn in der Form nnn. geschrieben, so faßt Mathematica sie als Gleitpunktzahl, also vom Typ ![]() , auf.
, auf.
Mit ![]() kann man den Typ einer Zahl x feststellen. So liefert
kann man den Typ einer Zahl x feststellen. So liefert ![]() , während
, während ![]()
![]() ergibt. Die reellen und imaginären Komponenten einer komplexen Zahl können beliebigen Zahlentypen angehören. Eine Zahl wie
ergibt. Die reellen und imaginären Komponenten einer komplexen Zahl können beliebigen Zahlentypen angehören. Eine Zahl wie ![]() wird Mathematica dem Typ
wird Mathematica dem Typ ![]() zuordnen, während
zuordnen, während ![]() vom Typ
vom Typ ![]() ist, da 0. als Gleitpunktzahl mit dem genäherten Wert 0 aufgefaßt wird.
ist, da 0. als Gleitpunktzahl mit dem genäherten Wert 0 aufgefaßt wird.
Es gibt einige weitere Operationen, um Auskünfte über Zahlen zu erhalten. So liefert
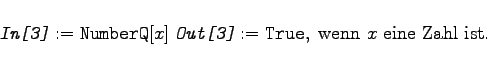 |
(20.7a) |
Anderenfalls ergibt sich ![]() Hier sind
Hier sind ![]() und
und ![]() die Symbole für die BOOLEschen Werte Wahr und Falsch .
die Symbole für die BOOLEschen Werte Wahr und Falsch .
![]() testet, ob x eine ganze Zahl ist, weshalb
testet, ob x eine ganze Zahl ist, weshalb
 |
(20.7b) |
ergibt. Ähnliche Tests für Zahlen sind mit den Operatoren ![]() ,
, ![]() und
und ![]() durchführbar. Ihr Sinn ist selbsterklärend. So ergibt
durchführbar. Ihr Sinn ist selbsterklärend. So ergibt
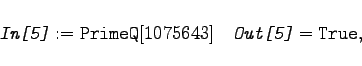 |
(20.7c) |
während
 |
(20.7d) |
liefert.
Die zuletzt genannten Tests gehören zu einer ganzen Gruppe von Testoperatoren, die alle mit ![]() enden und jeweils mit
enden und jeweils mit ![]() oder
oder ![]() im Sinne eines logischen Tests antworten (u.a. Typprüfung).
im Sinne eines logischen Tests antworten (u.a. Typprüfung).