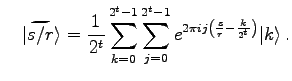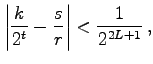Quantenalgorithmus zur Ordnungsfindung
Die Ordnung von 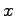 modulo
modulo 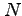 bezeichnet die kleinste ganze Zahl
bezeichnet die kleinste ganze Zahl 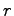 , so daß
, so daß  . Falls
. Falls 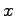 und
und 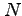 teilerfremd sind, ist die Funktion
teilerfremd sind, ist die Funktion  periodisch in
periodisch in  mit Periode
mit Periode 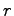 , d.h.
, d.h.  falls
falls  ein Vielfaches von
ein Vielfaches von 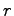 ist. Der unten beschriebene Quantenalgorithmus berechnet die Ordnung, indem er durch inverse FOURIER-Transformation die Periode der Funktion
ist. Der unten beschriebene Quantenalgorithmus berechnet die Ordnung, indem er durch inverse FOURIER-Transformation die Periode der Funktion  ermittelt.
ermittelt.
Es werden hierfür zwei Quantenregister mit jeweils  bzw.
bzw.  Qubits benötigt, wobei
Qubits benötigt, wobei 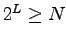 , so daß das zweite Register Zahlen von 0 bis
, so daß das zweite Register Zahlen von 0 bis  darstellen kann, während
darstellen kann, während  mit
mit 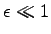 (siehe unten). Außerdem benötigt man einen Quantenschaltkreis, der folgende Operation auf den beiden Registern durchführt:
(siehe unten). Außerdem benötigt man einen Quantenschaltkreis, der folgende Operation auf den beiden Registern durchführt:
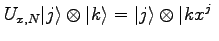 mod mod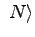 |
(22.28) |
und während des folgenden Algorithmus nur einmal durchlaufen werden muß.
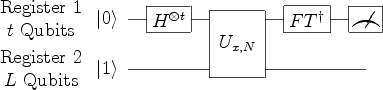
Der in nachfolgender Schaltkreis gezeigte Algorithmus verläuft wie folgt:
-
Initialisiere die Register im Zustand
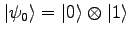
-
Wende

auf Register 1 an. Dies erzeugt den Zustand
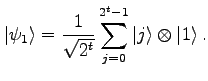 |
(22.29) |
-
Wende die Operation
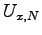
an. Dies erzeugt den Zustand
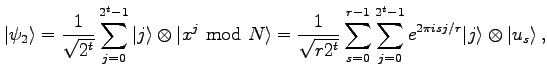 |
(22.30) |
wobei
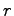
die gesuchte Ordnung von
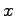
modulo
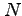
ist, und
 mod mod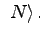 |
(22.31) |
-
Wende die inverse Quanten-F
OURIER-Transformation
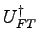
auf Register 1 an. Dies erzeugt den Zustand
 mit mit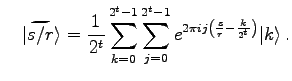 |
(22.32) |
Zu
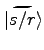
tragen nur Zustände
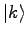
signifikant bei, für die
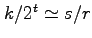
gilt.
-
Lies den Zustand
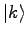
des ersten Registers aus. Mit Wahrscheinlichkeit größer als
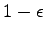
gilt nun:
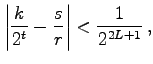 |
(22.33) |
wobei

eine durch den Meßprozeß zufällig ausgewählte Zahl zwischen
0 und
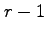
ist. Hierdurch ist der Bruch
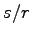
mit
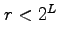
eindeutig bestimmt.
-
Bestimme den Nenner
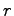
durch Darstellung von
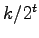
als Kettenbruch.
Zum Schluß wird geprüft, ob wirklich  gilt. Ist dies der Fall, dann war der Algorithmus erfolgreich. Der Algorithmus kann aber aus folgenden zwei Gründen auch fehlschlagen:
gilt. Ist dies der Fall, dann war der Algorithmus erfolgreich. Der Algorithmus kann aber aus folgenden zwei Gründen auch fehlschlagen:
-
Erstens könnte
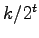
eine schlechte Näherung an
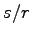
sein. Dies geschieht mit der Wahrscheinlichkeit kleiner als

, die durch Wahl eines genügend großen

(siehe oben) vernachlässigt werden kann.
-
Zweitens könnten

und
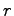
einen gemeinsamen Teiler
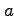
besitzen. In diesem Fall liefert die Kettenbruchdarstellung den Nenner

anstelle von
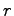
. Die gewünschte Ordnung
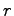
kann dann durch mehrmaliges Wiederholen des obigen Algorithmus ermittelt werden
[23.4].
![]()
![]() Quantencomputer Quanten-Algorithmen Shor-Algorithmus zur Primfaktorzerlegung
Quantencomputer Quanten-Algorithmen Shor-Algorithmus zur Primfaktorzerlegung
![]() modulo
modulo ![]() bezeichnet die kleinste ganze Zahl
bezeichnet die kleinste ganze Zahl ![]() , so daß
, so daß ![]() . Falls
. Falls ![]() und
und ![]() teilerfremd sind, ist die Funktion
teilerfremd sind, ist die Funktion ![]() periodisch in
periodisch in ![]() mit Periode
mit Periode ![]() , d.h.
, d.h. ![]() falls
falls ![]() ein Vielfaches von
ein Vielfaches von ![]() ist. Der unten beschriebene Quantenalgorithmus berechnet die Ordnung, indem er durch inverse FOURIER-Transformation die Periode der Funktion
ist. Der unten beschriebene Quantenalgorithmus berechnet die Ordnung, indem er durch inverse FOURIER-Transformation die Periode der Funktion ![]() ermittelt.
ermittelt.![]() bzw.
bzw. ![]() Qubits benötigt, wobei
Qubits benötigt, wobei ![]() , so daß das zweite Register Zahlen von 0 bis
, so daß das zweite Register Zahlen von 0 bis ![]() darstellen kann, während
darstellen kann, während ![]() mit
mit ![]() (siehe unten). Außerdem benötigt man einen Quantenschaltkreis, der folgende Operation auf den beiden Registern durchführt:
(siehe unten). Außerdem benötigt man einen Quantenschaltkreis, der folgende Operation auf den beiden Registern durchführt: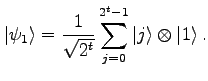
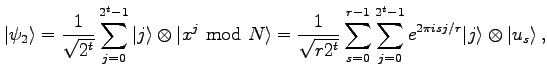
 mod
mod mit
mit