Sei ![]() eine Abbildung des metrischen Raumes
eine Abbildung des metrischen Raumes ![]() in den metrischen Raum
in den metrischen Raum ![]() . T heißt stetig im Punkt
. T heißt stetig im Punkt ![]() , wenn für jede Umgebung V=V(y0) des Punktes y0 = T(x0) eine Umgebung U=U(x0) existiert, so daß gilt:
, wenn für jede Umgebung V=V(y0) des Punktes y0 = T(x0) eine Umgebung U=U(x0) existiert, so daß gilt:
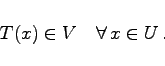 |
(12.76) |
T heißt stetig auf der Menge ![]() , wenn T in jedem Punkt der Menge A stetig ist. Äquivalente Eigenschaften zur Stetigkeit auf
, wenn T in jedem Punkt der Menge A stetig ist. Äquivalente Eigenschaften zur Stetigkeit auf ![]() sind:
sind: