Inhalt Index DeskTop Bronstein
![]()
![]() Vektoranalysis und Feldtheorie Räumliche Differentialoperationen Rotation des Vektorfeldes Definitionen der Rotation
Vektoranalysis und Feldtheorie Räumliche Differentialoperationen Rotation des Vektorfeldes Definitionen der Rotation
Zu einem Vektorfeld ![]() läßt sich ein zweites Vektorfeld, seine Rotation bilden, indem die folgenden Schritte durchgeführt werden:
läßt sich ein zweites Vektorfeld, seine Rotation bilden, indem die folgenden Schritte durchgeführt werden:
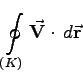 längs der Randkurve K des Flächenstücks.
längs der Randkurve K des Flächenstücks.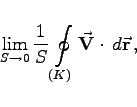
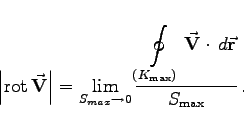 |
(13.56a) |
Die Projektion von ![]() auf die Flächennormale
auf die Flächennormale ![]() des ursprünglichen Flächenstücks mit dem Inhalt
des ursprünglichen Flächenstücks mit dem Inhalt ![]() , d.h. die Komponente des Vektors
, d.h. die Komponente des Vektors ![]() in beliebig vorgegebener Richtung
in beliebig vorgegebener Richtung ![]() , ergibt sich zu
, ergibt sich zu
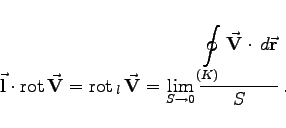 |
(13.56b) |
Die Feldlinien des Feldes ![]() werden Wirbellinien des Vektorfeldes
werden Wirbellinien des Vektorfeldes ![]() genannt.
genannt.