Inhalt Index DeskTop Bronstein
![]()
![]() Vektoranalysis und Feldtheorie Integration in Vektorfeldern Kurvenintegral und Potential im Vektorfeld Kurvenintegral im Vektorfeld
Vektoranalysis und Feldtheorie Integration in Vektorfeldern Kurvenintegral und Potential im Vektorfeld Kurvenintegral im Vektorfeld
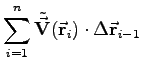 für
für 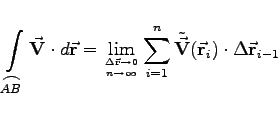 |
(13.96b) |
bezeichnet. Die Existenz des Kurvenintegrals (13.96a,b) ist gesichert, wenn die Vektorfunktion ![]() und das Bogenstück
und das Bogenstück ![]() stetig sind und wenn letzteres stetige Tangenten besitzt. Eine Vektorfunktion
stetig sind und wenn letzteres stetige Tangenten besitzt. Eine Vektorfunktion ![]() ist stetig, wenn die zu ihrer Beschreibung notwendigen drei skalaren Funktionen, ihre Komponenten, stetig sind.
ist stetig, wenn die zu ihrer Beschreibung notwendigen drei skalaren Funktionen, ihre Komponenten, stetig sind.