Inhalt Index DeskTop Bronstein
![]()
![]() Vektoranalysis und Feldtheorie Integration in Vektorfeldern Integralsätze
Vektoranalysis und Feldtheorie Integration in Vektorfeldern Integralsätze
Die GREENschen Integralsätze liefern Zusammenhänge zwischen jeweils einem Raum- und einem Flächenintegral. Sie ergeben sich aus der Anwendung des GAUSSschen Satzes auf die Funktion ![]() , wobei U1 und U2 skalare Feldfunktionen sind und v das von der Fläche S eingeschlossene Volumen.
, wobei U1 und U2 skalare Feldfunktionen sind und v das von der Fläche S eingeschlossene Volumen.
 |
(13.121) |
 |
(13.122) |
Speziell für U1 = 1 gilt:
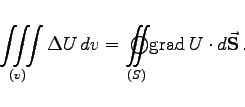 |
(13.123) |
In kartesischen Koordinaten hat der 3. GREENsche Satz die folgende Form:
 |
(13.124) |
| Beispiel A |
|
Berechnung des Linienintegrals: |
| Beispiel B |
|
Gesucht ist der Fluß |
| Beispiel C |
|
Wärmeleitungsgleichung: Die zeitliche Änderung des Wärmeinhaltes Q eines Raumteiles |