Inhalt Index DeskTop Bronstein
![]()
![]() Funktionentheorie Algebraische und elementare transzendente Funktionen
Funktionentheorie Algebraische und elementare transzendente Funktionen
Eine komplexe Funktion von einer reellen Veränderlichen t kann auch in Parameterform dargestellt werden:
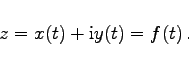 |
(14.91) |
Bei Änderungen von t durchlaufen die Punkte z eine Kurve ![]() .
.
Die Gleichungen für Gerade, Kreis, Hyperbel, Ellipse und logarithmische Spirale lauten:
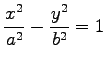
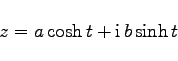 |
(14.94a) |
oder
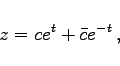 |
(14.94b) |
wobei c und ![]() konjugiert komplexe Zahlen sind:
konjugiert komplexe Zahlen sind:
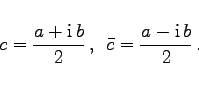 |
(14.94c) |
 :
: |
(14.95a) |
oder
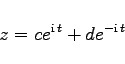 |
(14.95b) |
mit
 |
(14.95c) |
d.h., c und d sind beliebige reelle Zahlen.
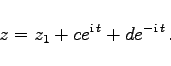 |
(14.96) |
Mit c und d sind beliebige komplexe Zahlen bezeichnet, die die Länge der Ellipsenachsen und ihre Drehung bestimmen.
 |
(14.97) |
wobei a und b beliebige komplexe Zahlen sind.