Eine Funktion
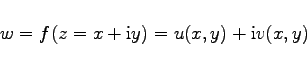 |
(14.31a) |
gilt als definiert, wenn die zwei Funktionen u(x,y) und v = v(x,y) reeller Veränderlicher definiert und bekannt sind. Die Funktion f(z) braucht nicht analytisch zu sein, wie das bei der konformen Abbildung gefordert wird. Die Funktion w definiert eine neue komplexe Zahlenebene. Man sagt, sie bildet die z-Ebene in die w-Ebene ab, d.h., jeder Punkt ![]() wird in einem ihm entsprechenden Punkt
wird in einem ihm entsprechenden Punkt ![]() abgebildet.
abgebildet.
| y | = | ||
| x | = | (14.31b) |
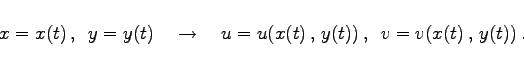 |
(14.31c) |
Mit t ist der Parameter bezeichnet.
| Beispiel |
|
Für Die schraffierte Fläche in der linken Abbildung wird auf die schraffierte Fläche in der rechten Abbildung abgebildet. |