Inhalt Index DeskTop Bronstein
![]()
![]() Funktionentheorie Integration im Komplexen Integralsatz von Cauchy, Hauptsatz der Funktionentheorie
Funktionentheorie Integration im Komplexen Integralsatz von Cauchy, Hauptsatz der Funktionentheorie
Wenn eine Funktion f(z) in einem einfach zusammenhängenden Gebiet analytisch ist, dann gelten die folgenden zwei äquivalenten Aussagen:
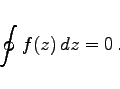 |
(14.40) |
 ist unabhängig von der die Punkte A und B verbindenden Kurve.
ist unabhängig von der die Punkte A und B verbindenden Kurve.Dieser Sachverhalt wird Integralsatz von CAUCHY, auch Hauptsatz der Funktionentheorie genannt.