Laurent-Entwicklung

Jede Funktion , die im Innern eines Kreisringes zwischen zwei konzentrischen Kreisen mit dem Mittelpunkt z₀ und den Radien r₁ und r₂ analytisch ist, kann in eine verallgemeinerte Potenzreihe, die LAURENT-Reihe, entwickelt werden:

f(z) =

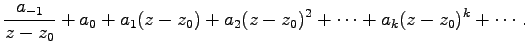+ (14.50a)

Die im allgemeinen komplexen Koeffizienten a_n sind eindeutig durch die Formel

bestimmt. Mit K ist irgendein geschlossener Integrationsweg bezeichnet, der innerhalb des Kreisringgebiets r₁ < | z | < r₂ liegt und im Gegenuhrzeigersinn durchlaufen wird (s. Abbildung).

Ist das Gebiet G der Funktion f(z) umfassender als der Kreisring, dann ist der Konvergenzbereich der LAURENT-Reihe der größte in G enthaltene Kreisring um .

Beispiel

Für die Funktion , die im Ringgebiet 1<|z|<2 analytisch ist, soll eine LAURENT-Reihenentwicklung bezüglich z₀=0 angegeben werden. Dazu kann man die Funktion f(z) durch Partialbruchzerlegung auf die Form bringen. Durch einfache Umformung können diese beiden Terme als geometrische Reihen dargestellt werden, die gemeinsam in dem Ringgebiet 1< |z|<2 konvergieren. Man erhält: