Berechnung eines speziellen bestimmten Integrals

Dem gesuchten reellen Integral wird auf folgende Weise ein komplexes Integral zugeordnet:
.
Das letzte dieser Integrale ist Bestandteil des komplexen Integrals . Die Kurve K besteht aus dem oben definierten Halbkreisbogen K_R und dem Stück der reellen Achse zwischen -R und . Der komplexe Integrand hat in der oberen Halbebene nur die singuläre Stelle . Nach dem Residuensatz gilt:
so daß

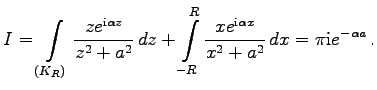
Aus ergibt sich unter Beachtung des Lemmas von JORDAN:
.

Auf ähnliche Weise wurden weitere Integrale der Tabelle Bestimmte Integrale berechnet.