Absoluter und relativer Maximalfehler
- 1. Absoluter Maximalfehler:
- Ist die zu bestimmende Größe z eine Funktion der Meßgrößen
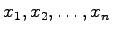 , d.h.
, d.h.  , dann muß der resultierende absolute Fehler unter Berücksichtigung dieser Funktion berechnet werden. Das geschieht entweder mit Hilfe des Fehlerfortpflanzungsgesetzes, wodurch ein Ausgleich der Messungen vorgenommen wird, weil nach der Fehlerquadratmethode ein Minimum von
, dann muß der resultierende absolute Fehler unter Berücksichtigung dieser Funktion berechnet werden. Das geschieht entweder mit Hilfe des Fehlerfortpflanzungsgesetzes, wodurch ein Ausgleich der Messungen vorgenommen wird, weil nach der Fehlerquadratmethode ein Minimum von  gesucht wird, oder man verzichtet auf den Ausgleich der Meßwerte und berechnet lediglich eine obere Fehlerschranke, die absoluter Maximalfehler
gesucht wird, oder man verzichtet auf den Ausgleich der Meßwerte und berechnet lediglich eine obere Fehlerschranke, die absoluter Maximalfehler 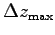 genannt wird. Für den Fall, daß es sich um n unabhängige Veränderliche xi handelt, gilt:
genannt wird. Für den Fall, daß es sich um n unabhängige Veränderliche xi handelt, gilt:
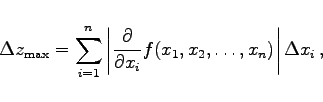 |
(16.216) |
wobei für die xi der jeweilige Mittelwert  einzusetzen ist.
einzusetzen ist.
- 2. Relativer Maximalfehler:
- Der relative Maximalfehler wird gebildet, indem der absolute Maximalfehler durch den Zahlenwert der Meßgröße (meist ist das der Mittelwert z) dividiert wird:
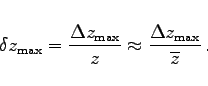 |
(16.217) |
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Theorie der Meßfehler Meßfehler und ihre Verteilung Meßfehlereinteilung nach quantitativen Merkmalen
Wahrscheinlichkeitsrechnung und Mathematische Statistik Theorie der Meßfehler Meßfehler und ihre Verteilung Meßfehlereinteilung nach quantitativen Merkmalen
![]() einzusetzen ist.
einzusetzen ist.