Es wird das Optimierungsproblem
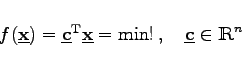 |
(18.114) |
über dem beschränkten Bereich ![]() , der mit konvexen Funktionen
, der mit konvexen Funktionen ![]() durch
durch ![]() beschrieben ist, betrachtet. Ein Problem mit nichtlinearer, aber konvexer Zielfunktion
beschrieben ist, betrachtet. Ein Problem mit nichtlinearer, aber konvexer Zielfunktion ![]() wird in diese Form überführt, indem
wird in diese Form überführt, indem
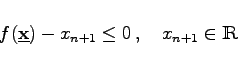 |
(18.115) |
als weitere Nebenbedingung aufgenommen und
 |
(18.116) |
mit ![]() gelöst wird.
gelöst wird.
Die Grundidee des Verfahrens besteht in der iterativen linearen Approximation von M in der Nähe des Minimalpunktes ![]() durch konvexe Polyeder, womit das Ausgangsproblem auf eine Folge linearer Programme zurückgeführt wird.
durch konvexe Polyeder, womit das Ausgangsproblem auf eine Folge linearer Programme zurückgeführt wird.
Zunächst wird ein Polyeder
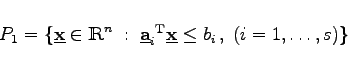 |
(18.117) |
bestimmt. Aus dem linearen Programm
 |
(18.118) |
wird ein bezüglich ![]() optimaler Eckpunkt
optimaler Eckpunkt ![]() von P1 erhalten. Ist
von P1 erhalten. Ist ![]() , dann ist die Optimallösung des Ausgangsproblems gefunden. Anderenfalls wird eine Hyperebene
, dann ist die Optimallösung des Ausgangsproblems gefunden. Anderenfalls wird eine Hyperebene
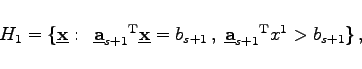
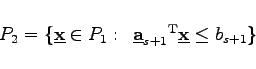 |
(18.119) |
erhalten wird.
Die Abbildung zeigt eine schematische Darstellung des Schnittebenenverfahrens.