Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Lineare Optimierung Grundbegriffe der linearen Optimierung, Normalform Ecke und Basis
Optimierung Lineare Optimierung Grundbegriffe der linearen Optimierung, Normalform Ecke und Basis
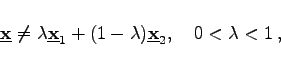 |
(18.7) |
d.h., ![]() liegt nicht auf der Verbindungsgeraden zweier verschiedener Punkte aus
liegt nicht auf der Verbindungsgeraden zweier verschiedener Punkte aus ![]() .
.
Unter der Annahme, daß der Rang von ![]() gleich m ist, können nur maximal m Spalten von
gleich m ist, können nur maximal m Spalten von ![]() linear unabhängig sein. Deshalb kann ein Eckpunkt höchstens m positive Komponenten besitzen. Die restlichen n - m Komponenten sind gleich Null. Im Normalfall sind genau m Komponenten positiv. Ist die Anzahl der positiven Komponenten jedoch kleiner als
linear unabhängig sein. Deshalb kann ein Eckpunkt höchstens m positive Komponenten besitzen. Die restlichen n - m Komponenten sind gleich Null. Im Normalfall sind genau m Komponenten positiv. Ist die Anzahl der positiven Komponenten jedoch kleiner als ![]() , dann spricht man von einer entarteten Ecke.
, dann spricht man von einer entarteten Ecke.