Basis

Jeder Ecke können m linear unabhängige Spaltenvektoren der Matrix zugeordnet werden, so daß darunter die zu positiven Komponenten gehörenden Spalten enthalten sind. Dieses System der linear unabhängigen Spaltenvektoren nennt man eine Basis der Ecke. Im Normalfall ist einer Ecke eindeutig eine Basis zugeordnet. Einer entarteten Ecke hingegen können im allgemeinen mehrere Basen zugeordnet werden. Es gibt höchstens 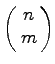Möglichkeiten, aus den n Spalten von m linear unabhängige auszuwählen. Demzufolge ist die Anzahl verschiedener Basen und somit auch der Ecken höchstens gleich 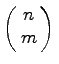. Ist M nicht leer, so hat M mindestens eine Ecke.

Beispiel

Der durch die Nebenbedingungen festgelegte zulässige Bereich M ist in der folgenden Abbildung dargestellt.

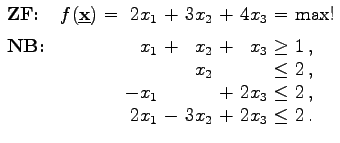Einführung von Schlupfvariablen führt auf:

Dem Eckpunkt des Polyeders P₂ = (0,1,0) entspricht im erweiterten System der Punkt
. Die Spalten 2, 5, 6 und 7 von bilden die zugehörige Basis. Dem Punkt P₁ entspricht die entartete Ecke (1,0,0,0,2,3,0). Eine Basis dieser Ecke besteht aus den Spalten 1, 5, 6 und einer der Spalten 2, 4 oder 7.