Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Lineare Optimierung Simplexverfahren Dualität in der linearen Optimierung
Optimierung Lineare Optimierung Simplexverfahren Dualität in der linearen Optimierung
Jeder linearen Optimierungsaufgabe (primales Problem) läßt sich umkehrbar eindeutig ein zweites Optimierungsproblem (duales Problem) zuordnen:
Primales Problem:
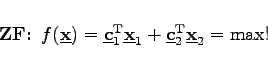 |
(18.19a) |
| + | |||
| + | |||
| (18.19b) |
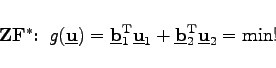 |
(18.20a) |
| + | |||
| + | |||
| (18.20b) |