Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Lineare Optimierung Simplexverfahren Dualität in der linearen Optimierung
Optimierung Lineare Optimierung Simplexverfahren Dualität in der linearen Optimierung
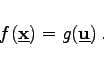 |
(18.21b) |
 |
(18.21c) |
An Hand der letzten beiden Beziehungen kann man aus einer nicht entarteten Optimallösung ![]() des dualen Problems eine Lösung
des dualen Problems eine Lösung ![]() des primalen Problems aus dem folgenden linearen Gleichungssystem ermitteln:
des primalen Problems aus dem folgenden linearen Gleichungssystem ermitteln: