Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Nichtlineare Optimierung Problemstellung und theoretische Grundlagen Optimalitätsbedingungen
Optimierung Nichtlineare Optimierung Problemstellung und theoretische Grundlagen Optimalitätsbedingungen
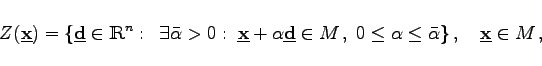 |
(18.34) |
wobei Richtungen mit ![]() bezeichnet sind. Ist
bezeichnet sind. Ist ![]() , dann liegen alle Punkte des Strahls
, dann liegen alle Punkte des Strahls ![]() für hinreichend kleine
für hinreichend kleine ![]() -Werte in
-Werte in ![]() .
.
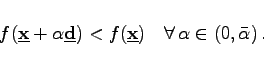 |
(18.35) |
In einem Minimalpunkt existiert keine Abstiegsrichtung, die zugleich auch zulässig ist.
Ist f differenzierbar, so folgt aus ![]() die Abstiegseigenschaft der Richtung
die Abstiegseigenschaft der Richtung ![]() . Mit
. Mit ![]() ist der Nablaoperator bezeichnet, so daß
ist der Nablaoperator bezeichnet, so daß ![]() den Gradienten der skalaren Funktion f an der Stelle
den Gradienten der skalaren Funktion f an der Stelle ![]() darstellt.
darstellt.