Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Lineare Optimierung Problemstellung und geometrische Darstellung Formen der linearen Optimierung
Optimierung Lineare Optimierung Problemstellung und geometrische Darstellung Formen der linearen Optimierung
Ein lineares Optimierungsproblem besitzt die folgende allgemeine Form:
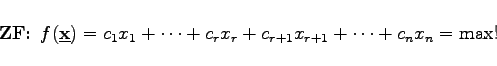 |
(18.1a) |
Abgekürzte Schreibweise: Die abgekürzte Schreibweise wird Kurzform genannt:
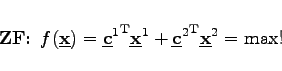 |
(18.2a) |
Dabei bedeuten:
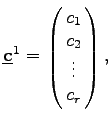 |
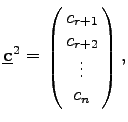 |
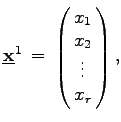 |
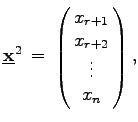 |
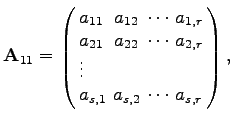 |
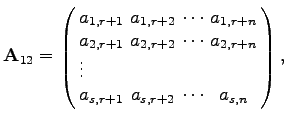 |
|
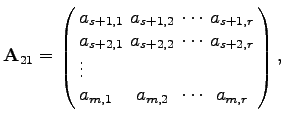 |
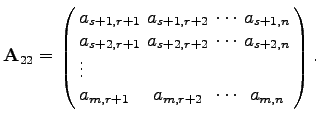 |
 |
(18.3) |