Formen der analytischen Darstellung einer Funktion
Funktionen von mehreren Veränderlichen können ebenso wie Funktionen von einer Veränderlichen auf verschiedene Weise angegeben werden.
- 1. Explizite Darstellung:
- Eine Funktion ist explizit dargestellt oder definiert, wenn sie durch ihre unabhängigen Variablen ausgedrückt werden kann:
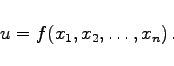 |
(2.269) |
- 2. Implizite Darstellung:
- Eine Funktion ist implizit dargestellt oder definiert, wenn die Argumente und die Funktion durch eine Gleichung der folgenden Art miteinander verknüpft sind:
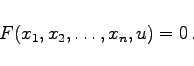 |
(2.270) |
Dabei wird vorausgesetzt, daß es zu jedem Wertesystem ( ) genau einen u-Wert gibt, so daß (2.270) gilt.
) genau einen u-Wert gibt, so daß (2.270) gilt.
- 3. Parameterdarstellung:
- Eine Funktion ist in Parameterform dargestellt, wenn die n Argumente und die Funktion durch n neue Veränderliche, die Parameter, explizit ausgedrückt sind, so daß für eine Funktion zweier Veränderlicher gilt
 |
(2.271a) |
für eine Funktion dreier Veränderlicher
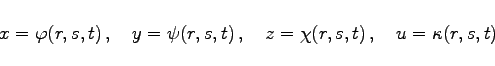 |
(2.271b) |
usw.
- 4. Homogene Funktion:
- Homogene Funktion wird eine Funktion
 von mehreren Veränderlichen genannt, wenn sie die Bedingung
von mehreren Veränderlichen genannt, wenn sie die Bedingung
 |
(2.272) |
für beliebige  erfüllt. Die Zahl m wird Homogenitätsgrad genannt.
erfüllt. Die Zahl m wird Homogenitätsgrad genannt.
| Beispiel A |
|
 d.h. Homogenitätsgrad d.h. Homogenitätsgrad  . .
|
| Beispiel B |
|
 d.h. Homogenitätsgrad d.h. Homogenitätsgrad  . .
|
![]()
![]() Funktionen und ihre Darstellung Funktionen von mehreren Veränderlichen Verschiedene ebene Definitionsbereiche
Funktionen und ihre Darstellung Funktionen von mehreren Veränderlichen Verschiedene ebene Definitionsbereiche
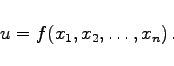
![]() ) genau einen u-Wert gibt, so daß (2.270) gilt.
) genau einen u-Wert gibt, so daß (2.270) gilt.
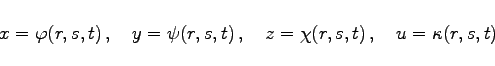

![]() erfüllt. Die Zahl m wird Homogenitätsgrad genannt.
erfüllt. Die Zahl m wird Homogenitätsgrad genannt.