Unbestimmte Integrale

Wenn zu einer gegebenen Funktion f(x) die Stammfunktion F(x) als Ausdruck elementarer Funktionen darstellbar ist, kann Maple diese nach dem Aufruf in der Regel finden. Die Integrationskonstante wird nicht ausgegeben. Ist die Stammfunktion Maple in geschlossener Form nicht bekannt, so gibt es den Integranden zurück. Maple kennt jedoch viele Spezialfunktionen und wird, sofern das möglich ist, diese für den Rückgabewert einsetzen. Anstelle des Operators kann auch die Langform benutzt werden.

Integrale gebrochenrationaler Funktionen

Beispiel A

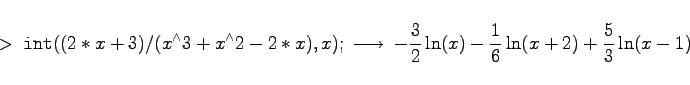Beispiel B

Integrale von Wurzelfunktionen

Mit Maple können die in den Tabellen Unbestimmte Integrale dargestellten Integrale entsprechend bestimmt werden.

Beispiel

Setzt man so findet man

Integrale mit trigonometrischen Funktionen

Beispiel A

Beispiel B

Hinweis:

Im Falle nichtelementarer Integrale (die auch durch dem System bekannte Spezialfunktionen nicht dargestellt werden können) wird lediglich eine Umformung vorgenommen.

Beispiel

denn dieses Integral ist elementar nicht darstellbar.