Inhalt Index DeskTop Bronstein
![]()
![]() Computeralgebrasysteme Mathematica Vektoren und Matrizen als Listen
Computeralgebrasysteme Mathematica Vektoren und Matrizen als Listen
Eine Reihe spezieller (Listen-) Anweisungen steht für die Definition von Vektoren und Matrizen bereit. Eine einstufige Liste der Art
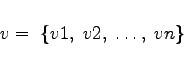 |
(20.13) |
läßt sich jederzeit als Vektor im n-dimensionalen Raum mit den Komponenten ![]() auffassen. Die spezielle Operation
auffassen. Die spezielle Operation ![]() erzeugt die Liste (den Vektor)
erzeugt die Liste (den Vektor) ![]() . Mit Vektoren dieser Art kann symbolische Vektorrechnung betrieben werden.
. Mit Vektoren dieser Art kann symbolische Vektorrechnung betrieben werden.
Die oben eingeführten zweistufigen Listen l1 und l2 können als Matrizen mit den Zeilen i und den Spalten j aufgefaßt werden. In diesem Falle wäre bij das Element der Matrix in der i-ten Zeile und der j-ten Spalte. Mit l1 ist eine Rechteckmatrix vom Typ (6,5), mit l2 eine quadratische Matrix vom Typ (5,5) gegeben.
Mit der Operation ![]() wird eine Matrix vom Typ (n,m) erzeugt, deren Elemente mit
wird eine Matrix vom Typ (n,m) erzeugt, deren Elemente mit ![]() gekennzeichnet werden. Mit i werden die Zeilen numeriert, i läuft von 1 bis
gekennzeichnet werden. Mit i werden die Zeilen numeriert, i läuft von 1 bis ![]() numeriert die Spalten und läuft von 1 bis
numeriert die Spalten und läuft von 1 bis ![]() . In dieser symbolischen Form läßt l1 sich darstellen:
. In dieser symbolischen Form läßt l1 sich darstellen:
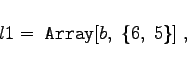 |
(20.14a) |
wobei für die Elemente gilt:
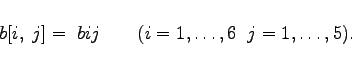 |
(20.14b) |
Die Operation ![]() erzeugt die n-stufige Einheitsmatrix.
erzeugt die n-stufige Einheitsmatrix.
Mit der Operation ![]() wird eine Diagonalmatrix mit den Elementen von liste auf der Hauptdiagonalen erzeugt.
wird eine Diagonalmatrix mit den Elementen von liste auf der Hauptdiagonalen erzeugt.
Die Operation ![]() gibt die Dimension einer Matrix, deren Struktur durch liste gegeben ist. Schließlich erhält man mit
gibt die Dimension einer Matrix, deren Struktur durch liste gegeben ist. Schließlich erhält man mit ![]() eine matrixartige Darstellung von liste. Eine weitere Möglichkeit zur Definition von Matrizen lautet: Es sei f(i,j) eine Funktion der ganzen Zahlen i und
eine matrixartige Darstellung von liste. Eine weitere Möglichkeit zur Definition von Matrizen lautet: Es sei f(i,j) eine Funktion der ganzen Zahlen i und ![]() . Dann kann mit
. Dann kann mit ![]() eine Matrix vom Typ (n,m) definiert werden, deren Elemente die jeweiligen f(i,j) sind.
eine Matrix vom Typ (n,m) definiert werden, deren Elemente die jeweiligen f(i,j) sind.