Operationen mit Matrizen und Vektoren

Mathematica ermöglicht die formale Manipulation von Matrizen und Vektoren. Dafür stehen die in der folgenden Tabelle aufgeführten algebraischen Operationen zur Verfügung.

Tabelle Operationen mit Matrizen

	die Matrix a wird mit dem Skalar c multipliziert
	das Produkt der Matrizen a und b
	die Determinante der Matrix a
	die inverse Matrix zu a
	die zu a transponierte Matrix
	die n-te Potenz der Matrix a
	die Eigenwerte der Matrix a
	die Eigenvektoren der Matrix a

Beispiel A

Es sei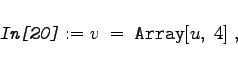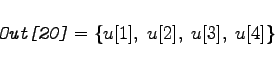

Mit

die zu r transponierte Matrix .
Definiert man den allgemeinen vierdimensionalen Vektor v mit

so erhält man

Nun kann das Produkt der Matrix r mit dem Vektor v gebildet werden, was bekanntlich einen neuen Vektor liefert (s. Rechenoperationen mit Matrizen).

Eine Unterscheidung von Spaltenvektoren und Zeilenvektoren gibt es in Mathematica nicht. Im allgemeinen ist die Matrixmultiplikation nicht kommutativ (s. Rechenoperationen mit Matrizen). Der Ausdruck entspricht in der linearen Algebra dem Produkt einer Matrix mit einem nachfolgenden Spaltenvektor, während dem Produkt eines Zeilenvektors mit einer nachfolgenden Matrix entspricht.

Beispiel B

Im Abschnitt CRAMERsche Regel ist das lineare Gleichungssystem pt=b mit der Matrix


und den Vektoren


behandelt worden. Da in diesem Fall det ist, kann man das System gemäß t=p^-1b sofort lösen. Das geschieht durch