Inhalt Index DeskTop Bronstein
![]()
![]() Computeralgebrasysteme Maple Prozeduren, Funktionen und Operatoren
Computeralgebrasysteme Maple Prozeduren, Funktionen und Operatoren
Der Operator der Differentiation lautet in Maple ![]() . Seine Anwendung erfolgt auf Funktionen in Prozedurform entsprechend
. Seine Anwendung erfolgt auf Funktionen in Prozedurform entsprechend ![]() bzw.
bzw. ![]() . Im ersten Fall wird die Ableitung einer Funktion von einer Variablen in Prozedurform bestimmt. Das Anhängen der geklammerten Variablen ergibt die Ableitung als Funktion. In anderer Form läßt sich dies als
. Im ersten Fall wird die Ableitung einer Funktion von einer Variablen in Prozedurform bestimmt. Das Anhängen der geklammerten Variablen ergibt die Ableitung als Funktion. In anderer Form läßt sich dies als ![]() schreiben. Höhere Ableitungen erhält man durch Mehrfachanwendung des Operators
schreiben. Höhere Ableitungen erhält man durch Mehrfachanwendung des Operators ![]() , was sich vereinfacht als
, was sich vereinfacht als ![]() schreiben läßt, wobei
schreiben läßt, wobei ![]() die n-te Potenz des Differentialoperators bedeutet.
die n-te Potenz des Differentialoperators bedeutet.
Ist G eine Funktion mehrerer Variabler, so erzeugt ![]() die partielle Ableitung von G nach der i-ten Variablen. Auch dieses Ergebnis ist wieder eine Prozedur. Mit
die partielle Ableitung von G nach der i-ten Variablen. Auch dieses Ergebnis ist wieder eine Prozedur. Mit ![]() erhält man
erhält man ![]() , d.h. die zweite partielle Ableitung nach der j-ten und i-ten Variablen. Entsprechend kann man höhere Ableitungen bilden.
, d.h. die zweite partielle Ableitung nach der j-ten und i-ten Variablen. Entsprechend kann man höhere Ableitungen bilden.
Für den Diffentialoperator ![]() gelten die aus der Differentialrechnung bekannten Grundregeln, wobei F und H differenzierbare Funktionen sind.
gelten die aus der Differentialrechnung bekannten Grundregeln, wobei F und H differenzierbare Funktionen sind.
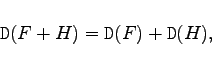 |
(20.51a) |
 |
(20.51b) |
 |
(20.51c) |