Auf alle Index-Qubits wird eine HADAMARD-Transformation angewendet, beginnend beim Indexzustand ![]() , wodurch der Zustand
, wodurch der Zustand ![]() in eine gleichförmige Überlagerung
in eine gleichförmige Überlagerung ![]() aller Index-Basiszustände
aller Index-Basiszustände ![]() umgewandelt wird:
umgewandelt wird:
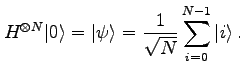 |
(22.25) |
Die GROVER-Unterroutine ihrerseits besteht, wie im untenstehenden Schaltkreis gezeigt, aus vier Schritten:
Diese vier Schritte können in der Gleichung ![]() zusammengefaßt werden, wobei
zusammengefaßt werden, wobei ![]() wie oben die gleichförmige Überlagerung aller Index-Basiszustände bezeichnet.
wie oben die gleichförmige Überlagerung aller Index-Basiszustände bezeichnet.
Schließlich wird der Zustand ![]() des Indexregisters ausgelesen, was durch Messung der Indexobservablen
des Indexregisters ausgelesen, was durch Messung der Indexobservablen ![]() geschieht. Das Meßergebnis
geschieht. Das Meßergebnis ![]() liefert mit hoher Wahrscheinlichkeit (s. unten) eine Lösung
liefert mit hoher Wahrscheinlichkeit (s. unten) eine Lösung ![]() des Suchproblems.
des Suchproblems.
Wie oft die GROVER-Unterroutine ![]() anzuwenden ist, um die Wahrscheinlichkeit für das Gelingen des Algorithmus zu maximieren, hängt von der Anzahl der Lösungen ab. Der Einfachheit halber kann angenommen werden, daß nur eine Lösung
anzuwenden ist, um die Wahrscheinlichkeit für das Gelingen des Algorithmus zu maximieren, hängt von der Anzahl der Lösungen ab. Der Einfachheit halber kann angenommen werden, daß nur eine Lösung ![]() existiert. 1 Wird die gleichförmige Überlagerung aller falschen Indizes
existiert. 1 Wird die gleichförmige Überlagerung aller falschen Indizes ![]() mit
mit ![]() bezeichnet, dann liefert die
bezeichnet, dann liefert die ![]() -malige Anwendung der Unterroutine
-malige Anwendung der Unterroutine ![]() auf den Anfangszustand
auf den Anfangszustand ![]()
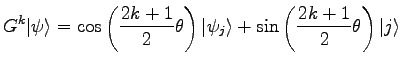 |
(22.26) |
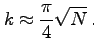 |
(22.27) |