Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Sphärische Trigonometrie Berechnung sphärischer Dreiecke Orthodrome
Geometrie Sphärische Trigonometrie Berechnung sphärischer Dreiecke Orthodrome
Für die Schnittpunkte ![]() und
und ![]() einer Orthodrome mit dem Breitenkreis
einer Orthodrome mit dem Breitenkreis ![]() ergibt sich gemäß (3.230):
ergibt sich gemäß (3.230):
Nach der NEPERschen Regel gilt für die beiden Schnittwinkel ![]() und
und ![]() unter denen eine Orthodrome mit dem nordpolnächsten Punkt
unter denen eine Orthodrome mit dem nordpolnächsten Punkt ![]() den Breitenkreis
den Breitenkreis ![]() schneidet:
schneidet:
 |
(3.237) |
Für den minimalen Kurswinkel ![]() muß das Argument in der Arkussinusfunktion hinsichtlich der Variablen
muß das Argument in der Arkussinusfunktion hinsichtlich der Variablen ![]() extremal sein. Man erhält:
extremal sein. Man erhält: ![]() d.h., in den Schnittpunkten mit dem Äquator ist der Betrag des Kurswinkels minimal:
d.h., in den Schnittpunkten mit dem Äquator ist der Betrag des Kurswinkels minimal:
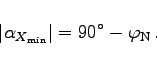 |
(3.238) |