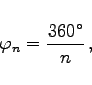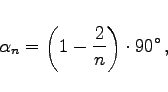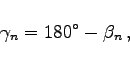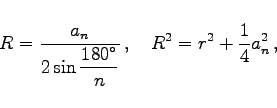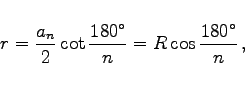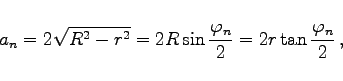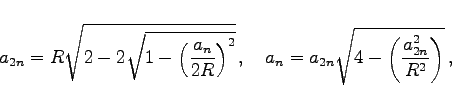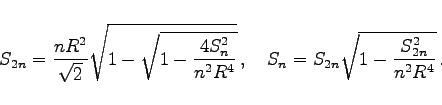Regelmäßige konvexe Vielecke haben n gleiche Seiten und n gleiche Innenwinkel. Der Schnittpunkt der Mittellote der Seiten des Vielecks ist der Mittelpunkt M des einbeschriebenen und des umbeschriebenen Kreises mit den Radien r bzw. 
. Die Seiten des n-Ecks sind Tangenten des Inkreises und Sehnen des Umkreises. Sie bilden um den Inkreis das Tangentenvieleck, im Umkreis das Sehnenvieleck.
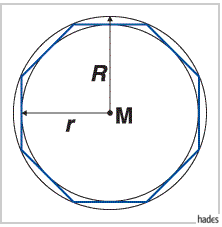
Die Zerlegung eines regelmäßigen konvexen n-Ecks ergibt n gleichschenklige kongruente Dreiecke um den Mittelpunkt 
, die Bestimmungsdreiecke.
Die Elemente des n-Ecks werden im folgenden durch den Index 
, die des 2n-Ecks mit dem Index 2n gekennzeichnet.
Für regelmäßige konvexe n-Ecke gelten die folgenden Beziehungen.
- Zentriwinkel:
-
 |
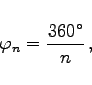(3.50) |
- Basiswinkel:
-
 |
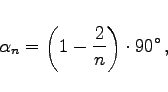(3.51) |
- Außenwinkel:
-
 |
(3.52) |
- Innenwinkel:
-
 |
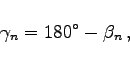(3.53) |
- Umkreisradius:
-
 |
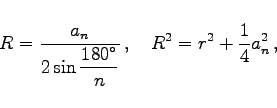(3.54) |
- Inkreisradius:
-
 |
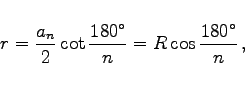(3.55) |
- Umfang:
-
 |
(3.56) |
- Seitenlänge:
-
 |
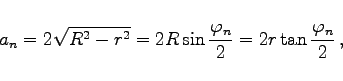(3.57) |
- Flächeninhalt:
-
 |
(3.58) |
- Beziehungen zwischen Seitenlängen und Flächeninhalten von n-Eck und 2n-Eck:
-
 |
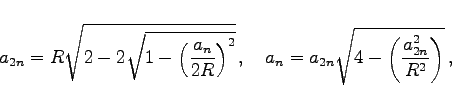(3.59) |
 |
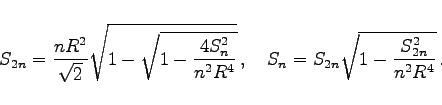(3.60) |
