Einige regelmäßige konvexe Vielecke

Die Eigenschaften einiger ausgewählter regelmäßiger konvexer Vielecke sind in der folgenden Tabelle zusammengefaßt.

Tabelle Eigenschaften einiger regelmäßiger Vielecke

	Seitenlänge a	Umkreisradius R	Inkreisradius r	Flächeninhalt S
3-Eck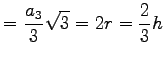
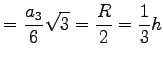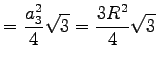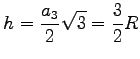5-Eck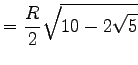
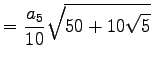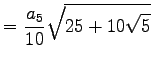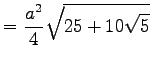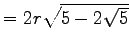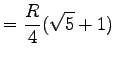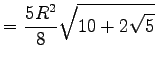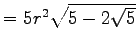6-Eck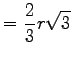
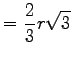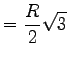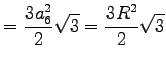8-Eck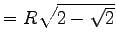
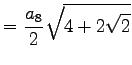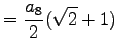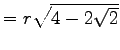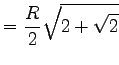10-Eck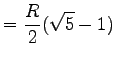

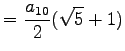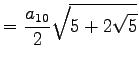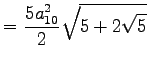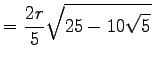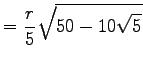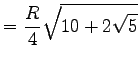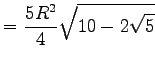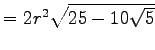Im folgenden Beispiel erfahren das Fünfeck und das Pentagramm eine spezielle Betrachtung, weil vermutlich an ihnen durch HIPPASOS von Metapont um 400 v. u. Z. die irrationalen Zahlen entdeckt wurden.

Beispiel

Die Diagonalen des regelmäßigen Fünfecks bilden einen Stern, das Pentagramm, dessen Inneres wieder ein regelmäßiges Fünfeck bildet.

Im regelmäßigen konvexen Fünfeck verhalten sich die Diagonale zur Seite wie sich die Seite zu Diagonale - Seite   verhalten: , wobei a₂ =a₀-a₁ ist.
Geht man analog zu immer kleineren eingeschachtelten Fünfecken mit und über, so gilt Der Euklidische Algorithmus für a₀ und a₁ bricht wegen , also nicht ab. Die Seite a₁ und die Diagonale a₀ des Pentagons sind somit inkommensurabel. Der sich für a₀:a₁ ergebenende Kettenbruch ist identisch mit dem Kettenbruch des Goldenen Schnittes, d.h. es ergibt sich eine irrationale Zahl.