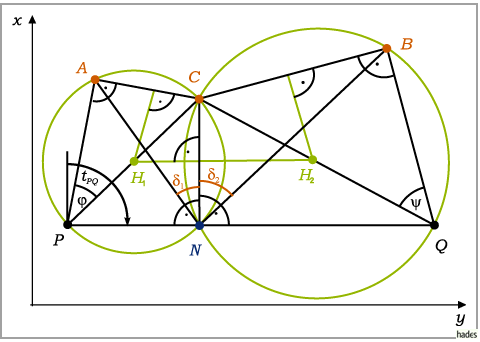
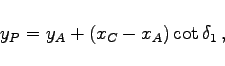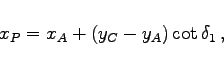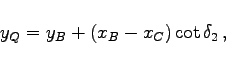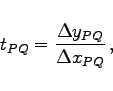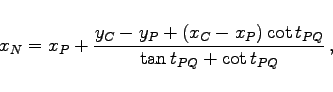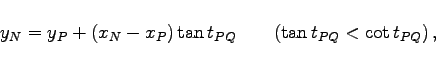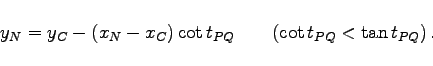Bei diesem Rechenverfahren werden zwei Hilfspunkte P und Q verwendet, die je auf einem Hilfskreis durch A,C,P bzw. B,C,Q sowie beide auf einer Geraden durch den Neupunkt N liegen.
Gegeben:  Gemessen:
Gemessen:  in
in  Gesucht:
Gesucht: 
Die Kreismittelpunkte H1 bzw. H2 sind die Schnittpunkte der Mittelsenkrechten von 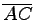 bzw.
bzw.  mit den Verbindungslinien PC bzw.
mit den Verbindungslinien PC bzw. 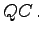 Die in N gemessenen Winkel
Die in N gemessenen Winkel  erscheinen wieder in P bzw. Q (Peripheriewinkel).
erscheinen wieder in P bzw. Q (Peripheriewinkel).
Lösung:
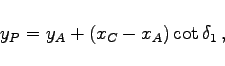 |
(3.117a) |
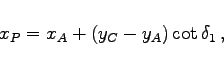 |
(3.117b) |
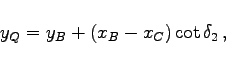 |
(3.117c) |
 |
(3.117d) |
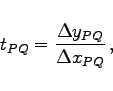 |
(3.117e) |
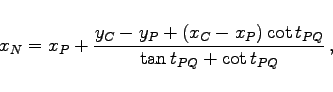 |
(3.117f) |
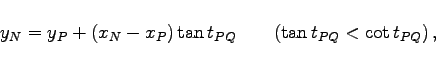 |
(3.117g) |
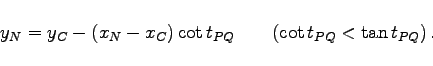 |
(3.117h) |
Gefährlicher Kreis: Bei der Punktauswahl ist dafür zu sorgen, daß die vier betrachteten Punkte nicht auf einem Kreis liegen, weil es dann keine Lösung gibt; man spricht vom gefährlichen Kreis. In dem Maße, in dem die Punkte in die Nähe eines gefährlichen Kreises zu liegen kommen, nimmt die Genauigkeit des Verfahrens ab.
![]()
![]() Geometrie Ebene Trigonometrie Geodätische Anwendungen Vermessungstechnische Anwendungen
Geometrie Ebene Trigonometrie Geodätische Anwendungen Vermessungstechnische Anwendungen
![]() Gemessen:
Gemessen: ![]() in
in ![]() Gesucht:
Gesucht: ![]()
![]() bzw.
bzw. ![]() mit den Verbindungslinien PC bzw.
mit den Verbindungslinien PC bzw. ![]() Die in N gemessenen Winkel
Die in N gemessenen Winkel ![]() erscheinen wieder in P bzw. Q (Peripheriewinkel).
erscheinen wieder in P bzw. Q (Peripheriewinkel).