Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Elementare Zahlentheorie Codierungen Fehlerkorrigierende Codes
Algebra und Diskrete Mathematik Elementare Zahlentheorie Codierungen Fehlerkorrigierende Codes
Eine nichtleere Teilmene ![]() heißt (binärer) linearer Code, wenn
heißt (binärer) linearer Code, wenn ![]() ein Untervektorraum von
ein Untervektorraum von ![]() ist. Hat ein linearer Code
ist. Hat ein linearer Code ![]() die Dimension k, dann wird er ein (n,k)-Linearcode genannt.
die Dimension k, dann wird er ein (n,k)-Linearcode genannt.
| Beispiel Fortsetzung |
|
|
Für binäre Linearcodes sind die Minimalabstände (und daraus die Anzahlen der korrigierbaren Fehler) leicht erkennbar: Der Minimalstand eines solchen Codes ist der kleinste Abstand eines Codewortes, das nicht selbst der Nullvektor ist, zum Nullvektor des Vektorraums. Man findet also den Minimalabstand, indem man die Minimalzahl![]() von Einsen in den Codewörtern ermittelt.
von Einsen in den Codewörtern ermittelt.
Für jeden (n,k)-Linearcode ![]() gibt es eine Generatormatrix G mit
gibt es eine Generatormatrix G mit ![]() :
:
 |
(5.289) |
Der Code ist durch Angabe der Generatormatrix eindeutig beschrieben; das Codewort zum Nachrichtenwort ![]() wird nach folgender Vorschrift bestimmt:
wird nach folgender Vorschrift bestimmt:
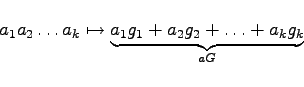 |
(5.290) |
Zum Decodieren benötigt man bei (n,k)-Linearcodes ![]() eine Kontrollmatrix H:
eine Kontrollmatrix H:
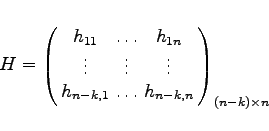 |
(5.291) |
Der (binäre) Linearcode ![]() ist (mindestens) 1-fehlerkorrigierend, wenn die Spalten von H paarweise verschieden und ungleich vom Nullvektor sind. Hat man in so einem Fall nach der Übertragung das Wort
ist (mindestens) 1-fehlerkorrigierend, wenn die Spalten von H paarweise verschieden und ungleich vom Nullvektor sind. Hat man in so einem Fall nach der Übertragung das Wort ![]() erhalten, dann berechnet man
erhalten, dann berechnet man ![]() . Ist das der Nullvektor, dann ist d selbst ein Codewort. Ansonsten stellt man fest, daß HdT die i-te Spalte hi der Kontrollmatrix H ist; das zugehörige Codewort ist dann
. Ist das der Nullvektor, dann ist d selbst ein Codewort. Ansonsten stellt man fest, daß HdT die i-te Spalte hi der Kontrollmatrix H ist; das zugehörige Codewort ist dann ![]() , wobei
, wobei ![]() ist und die 1 an der i-ten Stelle steht.
ist und die 1 an der i-ten Stelle steht.