Grundgesetze der Aussagenlogik

Zwei aussagenlogische Ausdrücke A und B heißen logisch äquivalent oder wertverlaufsgleich, in Zeichen: A=B, wenn sie die gleiche Wahrheitsfunktion repräsentieren. Folglich kann man mit Hilfe von Wahrheitstafeln die logische Äquivalenz aussagenlogischer Ausdrücke überprüfen. So gilt z.B. d.h., der Ausdruck hängt von A explizit nicht ab, was man schon an der obigen Wahrheitstafel erkennt. Insbesondere gelten folgende Grundgesetze der Aussagenlogik:

(1) Assoziativgesetze:

(5.8a)

(5.8b)

(2) Kommutativgesetze:

(5.9a)

(5.9b)

(3) Distributivgesetze:

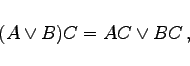(5.10a)

(5.10b)

(4) Absorptionsgesetze:

(5.11a)

(5.11b)

(5) Idempotenzgesetze:

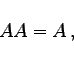(5.12a)

(5.12b)

(6) Ausgeschlossener Dritter:

(5.13a)

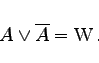(5.13b)

(7) DE MORGANsche Regeln:

(5.14a)

(5.14b)

(8) Gesetze für W und F:

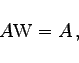(5.15a)

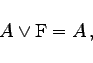(5.15b)

(5.15c)

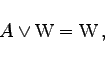(5.15d)

(5.15e)

(5.15f)

(9) Doppelte Negation:

(5.16)

Aus den Wahrheitstafeln für die Implikation und die Äquivalenz kann man erkennen, daß die Implikation und die Äquivalenz mit Hilfe der anderen Junktoren durch die Gleichungen

(5.17a)

und

(5.17b)

ausgedrückt werden können. Diese Gesetze werden zur Umformung (Vereinfachung) aussagenlogischer Ausdrücke verwendet.

Beispiel

Die Gleichung kann wie folgt bewiesen werden: