Inhalt Index DeskTop Bronstein
![]()
![]() Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Partielle Ableitungen
Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Partielle Ableitungen
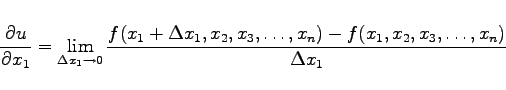 |
(6.35) |
definierte Differentialquotient, der zum Ausdruck bringt, daß nur eine der n Variablen variiert, während die anderen n - 1 dabei als Konstante betrachtet werden.
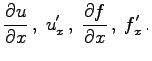 Von einer Funktion mit n Veränderlichen können n partielle Ableitungen erster Ordnung gebildet werden:
Von einer Funktion mit n Veränderlichen können n partielle Ableitungen erster Ordnung gebildet werden: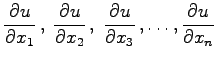 .
.| Beispiel |
|
|