Inhalt Index DeskTop Bronstein
![]()
![]() Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Extremwerte von Funktionen von mehreren Veränderlichen
Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Extremwerte von Funktionen von mehreren Veränderlichen
Eine Funktion ![]() besitzt im Punkt
besitzt im Punkt ![]() einen relativen Extremwert, wenn sich eine Zahl
einen relativen Extremwert, wenn sich eine Zahl ![]() derart angeben läßt, daß das Gebiet
derart angeben läßt, daß das Gebiet ![]() zum Definitionsbereich der Funktion gehört und für jeden Punkt dieses Gebiets mit Ausnahme von P0 für ein Maximum die Ungleichung
zum Definitionsbereich der Funktion gehört und für jeden Punkt dieses Gebiets mit Ausnahme von P0 für ein Maximum die Ungleichung
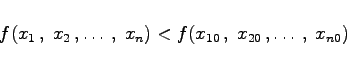 |
(6.69a) |
und für ein Minimum die Ungleichung
 |
(6.69b) |
gilt. In der Sprache des Begriffs des mehrdimensionalen Raumes sind in den Punkten eines relativen Maximums oder relativen Minimums die Funktionswerte größer oder kleiner als in den benachbarten Punkten.