Inhalt Index DeskTop Bronstein
![]()
![]() Unendliche Reihen Reihen mit konstanten Gliedern Allgemeine Konvergenzsätze
Unendliche Reihen Reihen mit konstanten Gliedern Allgemeine Konvergenzsätze
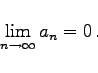 |
(7.20) |
Hierbei handelt es sich um eine notwendige, nicht aber um eine hinreichende Bedingung.
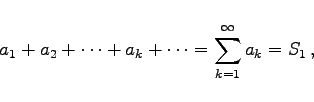 |
(7.21a) |
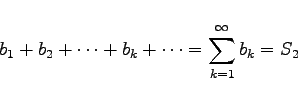 |
(7.21b) |
folgt die Konvergenz der folgenden Reihe mit der angegebenen Summe:
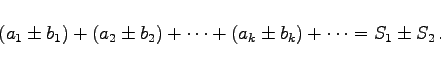 |
(7.21c) |
| Beispiel |
|
Für die harmonische Reihe (7.16) ist |