Inhalt Index DeskTop Bronstein
![]()
![]() Unendliche Reihen Fourier-Reihen Fourier-Reihe und Fourier-Integral
Unendliche Reihen Fourier-Reihen Fourier-Reihe und Fourier-Integral
Die Formel (7.106a) kann als Grenzfall der Entwicklung einer nichtperiodischen Funktion f(x) in eine trigonometrische Reihe im Intervall (-l,+l) für ![]() aufgefaßt werden.
aufgefaßt werden.
Mit Hilfe der FOURIERschen Reihenentwicklung wird eine periodische Funktion mit der Periode T als Summe harmonischer Schwingungen mit den Frequenzen  mit
mit ![]() und den Amplituden An dargestellt. Diese Darstellung beruht somit auf einem diskreten Frequenzspektrum.
und den Amplituden An dargestellt. Diese Darstellung beruht somit auf einem diskreten Frequenzspektrum.
Im Unterschied dazu wird mit Hilfe des FOURIER-Integrals die nichtperiodische Funktion f(x) als Summe unendlich vieler harmonischer Schwingungen mit stetig variierender Frequenz ![]() dargestellt. Das FOURIER-Integral liefert somit eine Entwicklung der Funktion f(x) in ein kontinuierliches Frequenzspektrum. Hierbei entspricht der Frequenz
dargestellt. Das FOURIER-Integral liefert somit eine Entwicklung der Funktion f(x) in ein kontinuierliches Frequenzspektrum. Hierbei entspricht der Frequenz ![]() die Dichte des Spekrums:
die Dichte des Spekrums:
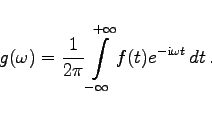 |
(7.106c) |
Das FOURIER-Integral ist von einfacherer Form, wenn die Funktion f(x) entweder a) eine gerade oder b) eine ungerade Funktion ist:
 |
(7.107a) |
 |
(7.107b) |
| Beispiel |
|
Für die gerade Funktion f(x) = e-|x| ergeben sich die Dichte des Frequenzspektrums und die Darstellung der Funktion zu |
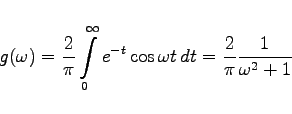 |
(7.108a) |
und
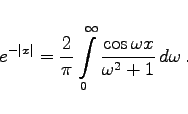 |
(7.108b) |