In der Tabelle FOURIER-Entwicklungen sind die FOURIER-Entwicklungen einiger einfacher Funktionen angegeben, die in einem bestimmten Intervall gegeben sind und darüber hinaus periodisch fortgesetzt werden. Der Kurvenverlauf ist für eine Reihe der entwickelten Funktion graphisch dargestellt.
| Beispiel |
|
Eine Funktion |
gegeben ist (s. Abbildung), kann auf die Form Nr. 5 in der Tabelle FOURIER-Entwicklungen gebracht werden, indem a = 1 gesetzt wird und die neuen Variablen Y=y-1 und 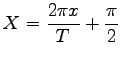 eingeführt werden.
eingeführt werden.
Durch die Variablensubstitution in der Reihe Nr. 5 der Tabelle erhält man wegen
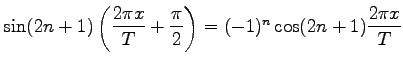 für die darzustellende Funktion (7.109a) den Ausdruck
für die darzustellende Funktion (7.109a) den Ausdruck
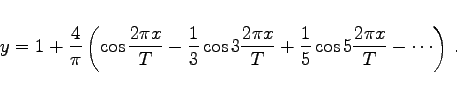 |
(7.109b) |
| Beispiel |
|
Die Entwicklung der Funktion |
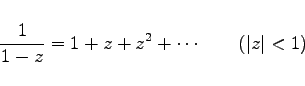 |
(7.110) |
liefert für
 |
(7.111) |
nach der Trennung von Real- und Imaginärteil
| = | 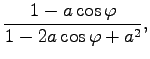 |
||
| = | 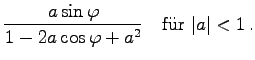 |
(7.112) |