Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Oberflächenintegrale Oberflächenintegrale 1. Art Begriff des Oberflächenintegrals 1. Art
Integralrechnung Oberflächenintegrale Oberflächenintegrale 1. Art Begriff des Oberflächenintegrals 1. Art
Oberflächenintegral 1. Art einer Funktion von drei Veränderlichen ![]() , die in einem zusammenhängenden Gebiet definiert sein muß, nennt man das Integral
, die in einem zusammenhängenden Gebiet definiert sein muß, nennt man das Integral
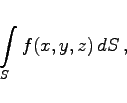 |
(8.148) |
das über ein im allgemeinen gekrümmtes Flächenstück S in dem genannten Gebiet genommen wird. Der Zahlenwert des Oberflächenintegrals 1. Art wird auf die folgende Weise ermittelt (s. Abbildung):
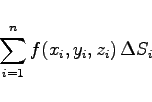 |
(8.149a) |
für den Fall, daß der Inhalt aller Elementarflächenstücke ![]() gegen Null geht, also ihre Anzahl n gegen
gegen Null geht, also ihre Anzahl n gegen ![]() . Dabei ist wieder zu beachten, daß der Durchmesser des Elementarflächenstückes gegen Null geht und nicht nur eine Ausdehnung.
. Dabei ist wieder zu beachten, daß der Durchmesser des Elementarflächenstückes gegen Null geht und nicht nur eine Ausdehnung.
Wenn dieser Grenzwert existiert und von der Art der Einteilung des Flächenstückes S in Elementarflächenstücke sowie von der Wahl der Punkte Mi(xi,yi,zi) unabhängig ist, dann wird er Oberflächenintegral 1. Art der Funktion u=f(x,y,z) über dem Flächenstück S genannt, und man schreibt
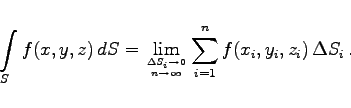 |
(8.149b) |