Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Oberflächenintegrale Oberflächenintegrale 2. Art Begriff des Oberflächenintegrals 2. Art
Integralrechnung Oberflächenintegrale Oberflächenintegrale 2. Art Begriff des Oberflächenintegrals 2. Art
Oberflächenintegral 2. Art einer Funktion von drei Veränderlichen ![]() , die in einem zusammenhängenden Gebiet definiert ist, nennt man das Integral
, die in einem zusammenhängenden Gebiet definiert ist, nennt man das Integral
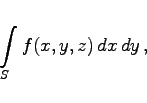 |
(8.156) |
das über die Projektion auf die x,y-Ebene eines orientierten, in dem gleichen Gebiet liegenden Flächenstückes S genomen wird. Der Zahlenwert des Integrals wird ebenso gewonnen, wie der des Oberflächenintegrals 1. Art, ausgenommen den dritten Schritt, bei dem der Funktionswert ![]() nicht mit dem Flächenelement
nicht mit dem Flächenelement ![]() , sondern mit dessen Projektion
, sondern mit dessen Projektion ![]() , orientiert auf die x,y-Ebene, zu multiplizieren ist. Damit ergibt sich:
, orientiert auf die x,y-Ebene, zu multiplizieren ist. Damit ergibt sich:
In Analogie dazu werden die Oberflächenintegrale 2. Art über die Projektionen des orientierten Flächenstückes S auf die y,z- und die z,x-Ebene wie folgt berechnet:
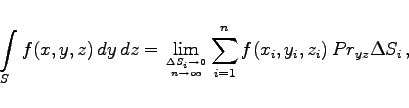 |
(8.157b) |