Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Bestimmte Integrale Grundbegriffe, Regeln und Sätze Eigenschaften bestimmter Integrale
Integralrechnung Bestimmte Integrale Grundbegriffe, Regeln und Sätze Eigenschaften bestimmter Integrale
Das Integrationsintervall [a,b] kann in Teilintervalle zerlegt werden. Der Wert des bestimmten Integrals über das gesamte Intervall wird dann gemäß
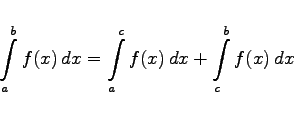 |
(8.43) |
berechnet (Intervallregel).
Besitzt der Integrand eine endliche Zahl von Sprungstellen, dann wird das Intervall durch sie in Teilintervalle aufgespaltet, in denen die Funktion stetig ist. Das Gesamtintegral kann mittels der Zerlegungsformel aus den Integralen über die Teilintervalle zusammengesetzt werden.