Exponentialgleichungen

Exponentialgleichungen können in den folgenden zwei Fällen auf algebraische Gleichungen zurückgeführt werden, wenn die Unbekannte x oder ein Polynom P(x) nur im Exponenten einiger Größen steht:

1. Sind die Potenzen nicht durch Additionen oder Subtraktionen miteinander verbunden, dann wird die Gleichung zu beliebiger Basis logarithmiert.
   

   Beispiel

   

2. Sind ganze oder gebrochene Potenzen ein und derselben Zahl k, d.h. ist
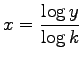   dann kann unter Umständen mit Hilfe des Ansatzes y = k^x eine algebraische Gleichung in y erhalten werden, nach deren Lösung x aus dem Verhältnis zahlenmäßig zu bestimmen ist.
   

   Beispiel

   
   Substitution von y = 2^x liefert y³ - 4y² - 32y = 0 und
   so daß daraus folgt Weitere reelle Wurzeln gibt es nicht.