Gleiche Annuitäten

Bei gleichbleibenden Tilgungsraten nehmen die zusätzlich anfallenden Zinsen im Laufe der Zeit ab (s. voranstehendes Beispiel). Bei der Annuitätentilgung wird dagegen zu jedem Zinstermin die gleiche Annuität A, d.h. der gleiche Betrag für Zinsen + Tilgung erhoben. Damit ist die Belastung des Schuldners im gesamten Tilgungszeitraum konstant.
Es werden die folgenden Bezeichnungen verwendet:

• S Schuld (Verzinsung mit pro Zinsperiode),
• A Annuität pro Zinsperiode
• a Tilgungsrate bei m Tilgungen pro Zinsperiode ,
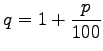• Aufzinsungsfaktor.

Als Restschuld S_n nach n Zinsperioden ergibt sich:

Dabei beschreibt der Term Sqⁿ den Wert der Schuld S nach n Zinsperioden mit Zinseszins (s. (1.79)), der zweite Term gibt den Wert der unterjährigen Tilgungsraten a mit Zinseszins wieder (s. (1.83b) mit E=a). Für die Annuität gilt:

Dabei entspricht die einmalige Zahlung von A den m Ratenzahlungen a. Aus der Gleichung folgt Da nach N Zinsperioden die Schuld getilgt sein soll, folgt aus (1.85) für S_N=0 unter Beachtung von (1.86):

Zur Lösung von Aufgaben der finanzmathematischen Praxis kann diese Gleichung nach einer der Größen A, S, q oder N aufgelöst werden, wenn die übrigen Größen bekannt sind.

Beispiel A

Eine Annuitätenschuld über werde jährlich mit verzinst und soll in 5 Jahren getilgt sein. Wie hoch sind jährliche Annuität A und monatliche Tilgungsrate a? Aus (1.87) bzw. (1.86) erhält man: , .

Beispiel B

Ein Kredit in Höhe von soll durch Annuitätentilgung in N=8 Jahren bei Jahreszinsen abgezahlt werden. An jedem Jahresende soll zusätzlich eine Tilgung von 5000.- Euro erfolgen. Wie hoch ist die monatliche Tilgungsrate? Als Annuität A pro Jahr ergibt sich gemäß (1.87) . Da sich A aus 12 Tilgungsraten a pro Jahr und die zusätzlichen Zahlungen von 5000.- Euro am Jahresende zusammensetzt, gilt unter Beachtung von (1.86) . Die monatliche Belastung beträgt somit .