Konvergenzsätze

In den folgenden drei Aussagen seien alle betrachteten Funktionen als LEBESGUE-meßbar vorausgesetzt.

1. Satz von B. Levi über die monotone Konvergenz:

Sei 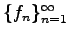eine fast überall monoton wachsende Folge nichtnegativer integrierbarer Funktionen mit Werten in . Dann gilt

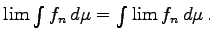
2. Satz von Fatou:

Sei {f_n} eine Folge nichtnegativer -wertiger meßbarer Funktionen. Dann gilt .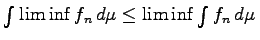

3. Satz von Lebesgue über dominante oder majorisierte Konvergenz:

Sei {f_n} eine Folge von meßbaren Funktionen, die auf fast überall zu einer Funktion f konvergiert. Wenn es eine solche integrierbare Funktion g mit 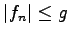fast überall gibt, dann ist f integrierbar und .