Für ein beliebiges (offenes) Gebiet 
bezeichnet 
die Menge aller in 
beliebig oft differenzierbaren Funktionen 
mit kompaktem Träger, d.h. die Menge
und liegt in 
, während mit 
die Menge aller bezüglich des LEBESGUE-Maßes im lokalsummierbaren Funktionen, d.h. aller (Klassen von äquivalenten) auf meßbaren Funktionen f mit 
für jedes beschränkte Gebiet 
, bezeichnet wird. Die beiden Mengen sind (mit den natürlichen algebraischen Operationen) Vektorräume. Es gilt 
für 
und für beschränktes auch 
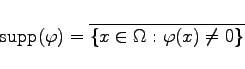
.Faßt man die Elemente aus 
als die von ihnen in 
erzeugten Klassen auf, so gilt bei beschränktem die Inklusion 
, wobei sogar dicht liegt. Ist unbeschränkt, so liegt (in diesem Sinn) die Menge dicht in .
Die Formel der partiellen Integration hat für eine vorgegebene feste Funktion 
und eine beliebige Funktion 
wegen 
die Gestalt
für 
mit 
, die man als Ausgangspunkt für den Begriff der verallgemeinerten Ableitung einer Funktion 
nehmen kann.
