Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Normierte Räume Begriff des normierten Raumes
Funktionalanalysis Normierte Räume Begriff des normierten Raumes
Sei ![]() ein Vektorraum über dem Körper
ein Vektorraum über dem Körper ![]() Eine Funktion
Eine Funktion ![]() heißt Norm auf dem Vektorraum
heißt Norm auf dem Vektorraum ![]() und das Paar
und das Paar ![]() normierter Raum über dem Körper
normierter Raum über dem Körper ![]() wenn für beliebige Elemente
wenn für beliebige Elemente ![]() und beliebiges
und beliebiges ![]() die folgenden Eigenschaften, die Axiome des normierten Raumes, erfüllt sind:
die folgenden Eigenschaften, die Axiome des normierten Raumes, erfüllt sind:
Mit Hilfe der Festlegung
kann jeder normierte Raum in einen metrischen so umgewandelt werden, daß die Metrik (12.81) zusätzlich noch die mit der Struktur des Vektorraums verträglichen Eigenschaften
besitzt. Somit stehen in einem normierten Raum sowohl die Eigenschaften eines Vektorraums als auch die eines metrischen Raumes - durch (12.82a) und (12.82b) verträglich aufeinander abgestimmt - zur Verfügung. Daraus ergibt sich, daß man die meisten lokalen auf einen Punkt bezogenen Untersuchungen mit den Einheitskugeln
 |
(12.83) |
vornehmen kann, da sich
 |
(12.84) |
ergibt. Außerdem sind die Operationen im zugrunde liegenden Vektorraum stetig, d.h., aus
Für konvergente Folgen schreibt man anstelle von (12.53) in normierten Räumen
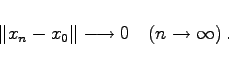 |
(12.86) |